從長度到實數的完備性

●師大數研所　林義雄

●說明線段長度的量度方法，介紹無理數的來源及實數完備性(極限觀念)，前半部適合高一，全部適合高三、教師。

§1長度

　　任取定一線段(比如：繩段、直尺)當作基準單位長度。據此，去比較另一線段或曲線的步驟，就稱為長度度量；然後，賦自該線段一個數目，稱為長度。長度是線段(或曲線)的內在性質。
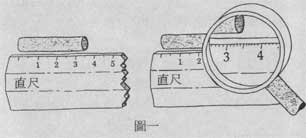
　　「度量長度」本身就是一種近似計算動作。約略地說，當您在比較之下覺得已量得正確長度時，如改用較精密的測長工具(比如：測微儀、顯微鏡、雷射槍等等)再重新度量一次，往往會發現到前次量得的長度只不過是一個"靠近"值而已。參考圖一。所使用的工具愈精密，量得的長度就會愈精確。對於人類的日常需要，通常只選用近似長度就足夠了。

§2線段的長度

　　同學們自小學開始所逐步建立起來的數線觀念，就是源自這種「長度度量」的行為，今略述如下。
　　在圖二中，取AB線段當作單位長度，它的(正)整數倍的長度就可刻劃上1,2,3,…,n,n+1,…( n 是自然數)。

　　假設一線段CD不是AB的整數倍，但是介於n倍及(n+I)倍之間。這是說，C及D之間有一點E使得CE長度是n(單位)，而ED長度不足一單位長，如下圖三。

　　問題是：如何在單位長度AE之限制下，去度量ED的長度？換句話說，如何給ED一個"數目"，使得它跟AB(即 1)可比長？分二種情形來討論。
　　第一種：在圖四的直角三角形EEG中，設EE = AE(=單位長)。如果存在一自然數p使得斜邊EG恰是p單位長，將EG p等份，從每一分點作EF之垂線(即正投影)。若D點怡是第q個分點的垂足，按初等幾何學相似三角形對應線段成比例，如
　　　　ED : EF = q : p 或 ED : 1=q : p
得到（單位）。
　　用相反的步驟，可以將正有埋數標示在線段上，即可找到一線段CE使得其長度怡為給定的正有理數。因此，有理數是可度量的數。。" 注意:在圖四中，邊EG可以不必垂直於邊它F:而且。可用圓規直尺達到分點及作平行線的操作。 另一方面，乃F:EG=I:p成立。這表示將乃F擴大戶倍成百C時。如刀點恰擴大到EG的第4個等分點，則本來的刀點在RF中佔7旦份;這邊等於說， 力將Ef力等分，則乃點恰好足第q個等分點。代表數值旦。 戶 第二種:(在圖四中)不論將Ef如何等份，乃都不曾往等分點上。 直觀上。EL是有"長度"的，介於O及I之間(註:規定一點的"長度"為0);但足，在有理數(或有限、循環小數)的知識範疇內，刮沒有辦法賦與一個數目。怎麼辦? 比如說:將EFIOOO0等份，發現到刀點介於第I532個等分點及第I53S個等分點之間，郎誌詫色二0．I532匕ED(長度)<0.I53S二品馬莘八參考圖五: 將該二等分擴大in倍之後。冉I0等份(郎EFI00000等份)，發現D點介於第8個等份點及第9個等分點之間，即再將這二個新分點擴大IC倍，然後IC等份(即EFIOOO0OC等份)，發現刀點介於第6。7等分點之間 即@口如此一直下去，-,D永遠不在等分點上。 但是，我們劫發現到R刀長度介於土、下二列有理數(可度量數)之間，即:仔細分析上述主客觀情勢，有(注意:在取定單位長方B{圖二)的大前提下) @)<主觀)要求EL的長度，但沒法用有理數(有 限小數)來表示。即F乃是不可度量的; 仞(客觀)可找到二列有理數(即可度量的線段長 度):一個是上升的0.I532，0.t5328，0.t53286， …;另一個是下降的0.I533，0.I5329,0.@53287， …滿足: 1a1這二個已知數列將未知的EL前後夾在中間( 如2式); (b1數列對應項的差為:這些事實告訴我們:雖然EL不可度量(□)，但是可用可度量的、已知的數來逼近未知的FD((@(a)):而且，逼近的程度可用已知的數來衡最((@@(b))，這是說，如用0。I53287或0．I53286來當作F刀的近似值，則EL真正的"長度"跟近似值的誤差不曾超過0．00000匕模仿山式的方法，到第竹個步驟，可得到有理數a.，阮滿足:因此，可取EL的近似值0n(或扒)，使其誤差小於預先任意設定的小數七古 好，什麼是FD的"長度"? 利用「客觀因素」來衡量「主觀情事」 用「已知」求「未知」，(心智活動)規定F刀的長度為由其 """近似值構成的有理數列: (0。I532，0．I5328，0．魄286，-，dn，-) (4)或是 t0．I533，0．I5329，0．I53紀 -，叭，-) (4)，如果一個人用儀器量得F刀的"長度"是0I53287，那不是FD的真正長度，僅是近似長度而已，而且誤差小於I。E刀的真正長度(4-或(4)是一種抽象的數學觀念，不可能用有理數(部有限或循環小數)來表達。但是，可取得有理數a,或扛任意靠近EL的真正長度如3式，此時記成百刀長度二廿ma,<從左邊靠近)@@稱為a.或玩的極限值，而這種步驟屬於極限觀念。"。'，通常，籠統地稱EL的長度((4)或凹或(5):是一種非循環的無限小數。將小數點後第%位所決定約有限小數記成a,，則(5)式就會成立了。s3真的有「不可度量長度的線段」或「不可度量的數」存在嗎?在s2的第二種情形，我們先假設「不論將單位長FE如何等分，乃都不會在等分點上」之大前提下，然後再說明EE是不可度量長度的線段。這導致利用「線段十等份」的技巧，從「已知」逐步求「未知」的方法，於是產生了「近似值」、「誤差」、「有理數列」、「極限值」、「非循環無限小數」的觀念。問題是:員的有這種線段存在嗎?有污而且，大多數的線段都是這種不可度量長度的線段。"給三個例子。喇1:古希臘人利用畢氏定理得知石田的斜邊AC不可度量。這是說，雖然C但是不能用單位長HB為出發點，賦與人C一個有理數"。 由於I之力C二2，將圖二由I到2的線段十等份，如同s2，可得到近似值數列，上下夾攻力c如: I二I．4弋I．4I二I．4I4二I．4I屹丈… 弋HC弋…丈I．4I43二I4I5二I。42 二I．5二2 (7)如何求下一步的近似值?將I．4I42到 ，4I43的線段十等份:每等份長度:二(1.4I4;一I．4I42'I0二三-X0.000]二0.0000I(8)皿等份點:I.41420，I.4I42I，I.4I422,．I.4I429.I．4I430將每個等分點的數目平方(因須借助(6)式的AC'二2，才能比較大小)，發現到: I．4I422一I．4I42I二0．叨00I二寺如此下去，可求得有理數0x及阮使得0x丈力C弋"而且扒一dn二 0□ (%是任給定的自然數)。情況完全如同s2中乃刀所對應的(2)、(3)式;於是，超星AC長度二有理數列付，I．4，I。4]，I，4I4,@.4I42I,-，0.,-，)二有理數列(2，I．5，I．42，I．4I5，仞@.4]偽，I.4I422,"，九，...)二lima,(從左邊靠近)，-@ 二 tm ，(從右邊靠近) 卜@@特記這個長度為叮2。


評註:利用下列圖餾我們可造出很多「不可度量長度的線段」，如同例I的方法，可賦與長度，通記成什丁(a是正有理數，但不是完全平方數)，稱為d的平方根，是「不可度量的數」的一種。逐次別用開平方根運算，配合加、減、乘、除，可得蛟複雜的「不可度量」的"數"，如下: 只有這種形狀的"數"，才可用直尺及圓規作出一線 段，其長度恰等於它。" 借助其他曲線(比如拋物線、歧點蔓葉線等等)， 可造出諸如乍三這種「不可度量」的"數"。"剛2:以單位長當半徑作一圓，則圓周長為何扒。'。"。。' 這是有名的圓周率元的問題。I值的估計一直足古 今中外人類數學活動的重要一環。魏國時代的劉徵用 園內接正3072邊形，得到T的近似值3．I4I59;後來到了I882年Lindemann證明r是一種「不可度量」的數(即不可表示成正有理數)。後來，'很多人從事兀的近似值計算;特別，當電子計算機問世以後，更有顯著的成就。在I982年，Y．Tamura及Y．Kanada利用十九世紀初葉Gauss-LegendreAlgorithm 之理論，藉助電子計算機算得I的近位值，精確到小數點後第4I94239位。今列出r到小數點後第5000位近似值的前、後段如下:3.I4I59265358979323絀6-"80998886874I3260472I試問這一生當中能有機會用到r的近似值嗎?用到第幾位? 並非所有「不可度量」的數，皆明顯地源自幾何作 圖。從自然界放射性物質的蛻變或是人口成長情況， 或是儲蓄利率成長的情況，也可引進這種數，請看例。w慨3:設本金是I，年利率是I00%，在一年當中分 成竹個相同的期間複利計算本息，則全部竹期 須付出本息為。"列表計算近似值(到小數點第五位)如下化又如何?至少，它的取值會不超過一個固定常數嗎J.Napier(I550-I6@7)曾計算當%二IOOOOOC時，對應的值為2．7I828I82…。為要回答前段的問題，我們利用二項式定理"，有

應項，得到 a,二乙n+i，m二I，2，3，-(II:當%妄2時，I一芸<I成立，I乏g乏%一I。所以，由 I一百 I 二I4 寺 丈I十二□三 一二3 I I 一了 一百綜合@l)、似式，得到 2二a@二az之a3之-<an弋0n+，之…之3 胸這表示不論%有多大，dn二(I+@)"的值不曾超過3。 L．Euler(@707-@789)用"表示n充分大時，a,所趨近的"數"，即令 g=lim(I十工)。 -@ ， 釘並計算e的值到小數點第23位。c．Hermite(I707-@789)證明e是「不可度最」的數(即不是有埋數)。e的前I?.位小數是 e=2.7I828I828459045．到了I955年，用電子計算機已算到小數點後第6萬位了。准平註:從10:式，容易得到 I @@ e二Hm乙十了) =li血(I十丰 十共十…十去)二二去 n□。 工． 2． "． "@，刀． I.@.@, @6 二@4-五十五十可 十…十叫"，0弋p二I叫據此，較容易計算e的近似值。比如:當取n=I0時 ，得近似值2．7@828I8]。而且，據此，容易證明e不是有理數，試試看。 這個e是自然對數的底數，在木書高中數學O中對於T，e將有專節討論。練習 :山設您的身高是I．5公尺。1a;在成長過程中，曾經 體會到在那一瞬間您的身高恰是心 二公尺嗎?可以 避開心 三公尺的身高作跳躍式的成長嗎?(b1如想堅 持您的身高曾經是心 三公尺，試問您要如何向同學 ，朋友把這件事情交待清楚到令人心服口服的程度 ?C1從您出生的身高到I．5公尺，您曾經歷到多少 個像叱丁公尺這種令人迷惑的身高?能學得出in個 情況嗎?(2)已知線段F@!滿足ED'=I7。何用十等分法，求ED 的近似長度，精確到小數點第3位。1b)如要給ED 長度一個數目，讓如何做?(3)用十等分法，求們 云的近似值，精確到小數點第3 位 立。(4)在十等分法中，試問那些有理數可表示成有限小數 了那些可表示成循環小數了"(5)如改成名等分法(g是大於I的自然數)，則固的 結果又如何?"。。'"(6)十等分法(郎iO進位制)中的有理數，會是名等分 法(即耳進位制)中的有理數嗎?反之，又如何? @3l(93"仞找□木有關圓周率K的歷史書，看看其演變過程。"(8)證明叫式。並證明e不是有理數。 s4「不可度量長度的線段」或「不可度量 的數」所代表的無理數 暨實數系的完 備性 。 綜合圖二、三及s3的例卜2，列表如下:可度最長度可將線地之端淺蟋在可表示成有可表示成有限或循環的線段某些等佛七上理數小數不可度呂長不可能將線段之端點不可以表示可表示成(非循環)度的線段擺在任意的等份點上成有理數妞限，1)數因此，規定(a是整數,叭,a@,-，a,。．‥是0，I，…，9當中的數目)無理數二非循環無限小數形如".1210203，‥Q" …蚵以表示「不可度量長度的線段」的長度，如吋刀"等等;或是，用以表示「不可度量的數」，如s3例3的e等等。如何對待一個無理數?令x二0．勺&z-a"．‥是一無理數，則最起碼要認識到:F有理數&．叱02．-8n並不等於x，僅是x的一個近似值而已;2。誤差，一0digz…a,二0.00。‥00n+i么h+，-I十…二而h%=I，2，3，。可按需要控制在任預定的小數之內。人類僅能用無理數的近似值;到目前為止，人類發明


的機恐尚沌螂汪列出小數點後所右的數口(it以口\2。行。f等等)"'。總而，之，妞理數岳/、絀從現甯肚，叫悅悟、淨止出來的一稱L智活動的咬約(看右 """""叫、仙'。向;(a@的兮五)。 今。規定餞數如下: 吆 ;有理鞍(有限小邀或涌碌叫．數) 日數 " 奸埋鞍(井待濁妊眠刁、數)並枝涌常的扣、沌、丰。除、開十力)方等等淨半，刁加U山由引用。金體的舀數均戍研老的庹魏忍"。 心一條亡細．上，取吶出文定引0弋.@@，規定裸段O．4/，一單匝R，出固，-。四的方江，可以將全紡的有埋數慄小在亡紳上，如下岡九; @下：．．@UD@吋C，卜@｜九月整八匕，*L4逗﹂百匕﹂@-@．，丁卡 十八心．｜．一曰@記上口．勺申山卒．芷數=;生理而吧口質山;．｜丁．里屯涼 @@乍屯?;叫出仇 H沁H純二--已．剛H一 一洲一一一一一一一@． ．-｜4E仕旺 仙L ｜， "。．-几芒吭叫：．- ｜" 伙R匕吋．叫．-廿往 -：汎Y毛直紉卯匕一口-，O一俘毛C泣兀，，工心啤-的U八七□迦。旺把""分氓丁﹄"汁：．、伙倍洲-@"乙．．．姦枕絆呻 ｜，須汎几扒人．．炬的沁、．： ． …口; 分。I皂．．"日和扒芷。的一侶，、，一系分J｜ 一． ｜刪咽忙洲腕圳川-一刑糾。．-．弋。 代，0心衍7山列的五安．1'!;'@ ．．L ．心弋r@i，乙@.，叩足舀數。，小;心的心，下，餞歡系朽下 ，叭.．‥:D，,阮，1H心。，1a，刁。 7"二，二二□n@ "7@口H:．什︶口凸亡｜，口白匕p臼仟人丁叮Q一一七P．即L ， 萃｜L｜L7@@凸。@純｜口｜打口｜，~．@卜@．． 一｜一 @PmU 口 Q 而 自 ｜H出@@@~一｜m。@一刀叫@｜ @二"@丁口｜@@ ｜- 4E @@妨甲L、@@L｜住年一口@ ｜ 巴刀｜｜一@，H， 弄激屑｜日Y，一。三臼 +卜，｜C-@，．， 。@卜刁． ｜ ｜，@，｜，上叭釗 -@．一口[p自白U 這二仙性茁液比勺三冉。挖此，稱舀數系民有完備門 ，蕊於咒鞍系譯細的討論及往，;泄程。呵看理論分寸 叫*第二草"， 練習: 小□旺皂R祝段笛作單位巨，旺色至仕「不可度討片 宅的神段」叫? 山什!;。八中，如□斜洩「比尚仟單仕三，則A@七三?'甘8;詳"叱、呻八，s5長度作為線段的函數觀念 。 從N-仁盯，研，山市引人私舛統，使行污一一線段，扒巴往;印對姓於11．一吋段，九十帖-．汕一倆蔽口叫之判匕，N人@、，，千k:F沙H:1仁往。□止，片唉J己:%八f*@@u;山!紉:，記以 /，(.4月)二二月竹扒、屯 帕。冉H，心釣，如卜岡卜:AI．忱)二I．7。 @，。，;恕巴石卜扒二仙牡本什，:: 伴凶I(軍匕恬茹):出竹;JR段汕H毛等竹I。 什心2(可印伴苟):山二條絲段瑞糾柏按組成的固衫乙如"!．．…)，共R哇莘伙""．純段L哩之和，川 /@(L@B口月C):L(AB)+/@(BC)什心3(不沒性"):紐段之尺度趴仟H照關，即如AJ月企芋竹T@@'，如釗-1．，，則


L(AB)二L(@'.6': 利用上述三種性質，可求得多邊形線段以致於曲線段的長度，我們將其衍發過程置於練習中，選讀者享受其樂趣。習題:山右圖十三是角邊長為I的正五邊形。 (a1求對角線之長(答:工(什 豆+I)); z 付求內部正五邊形之角邊長; 1C)求AB@AzB@之邊長;\@\@/ 匕///月 、 八几 ，@@ Y/、V/@A/I ，(C)作內部正五邊形的對角線， h戶戶入叫7 @A 再圍成一個更小的正五湧形 ' ，如此第(%一I)次之後所 圖十三 得竹正五瀋形記成H"B"．‥。水邊長刀"B"=9 求和式A@B，+凡Bz+…十月"B@，:?當n~四 時，結果如何?(2)給半徑為r的圓如石圖 十凹。造圓外切及圓內 按正六邊形。 V上 几 ，ZZ 固計第二仙六邊形的周 弋LL /夕/ 長(到小數點第3位 、己三主三刁 圖十匹 )。 心將固中所得的結果彼此互相比較之，再跟圓周長 互相比較。 1c)如邊數增多時，您認為結果孩如何?Y3)圓周長比值徑是個常數，稱為圓后率。試分別造半 徑為I，2，3，4，5，6，7，8的圓，依您 自己方法儘貝精確地量出對應的圓周長，以驗證這 個事實。如何給予嚴密證明? (4)取每邊長皆為I的正方形ABCD，取對邊中立百， F。以E為心，FC為半徑畫弧交AD於G點，作 矩形ABHG，稱為黃金矩形，如 、圃十五。，，，。(a)求AC之長度，通稱比AG:AB=AG為黃金比。肋證明DCHG邊是一個黃金矩形(即CD:DG=黃 金比)。(51求右圖十六圖形之邊界長，並 指明在何處用到什麼基木長度 性質。 "= 邸碎展．(6)設地球牛徑是I2800公里。今 用一環帶緊貼赤道繞一圈，如 圖十六 將環帶剪斷並增加長度I0公尺，然後再繞赤道一圈 ，但要求赤道上每一點 到環帶都等距離，如右 圖十七。問:(a]可在環 帶下伸入手指頭嗎? 付能在環帶底下爬行嗎? (01站起來行走嗎? U在底下駕汽車嗎? 圖十七 □前者皆不可以口(71試提出一些構想，列出一些步驟，以求得下列各曲 線之長度:s6參考資料山林義雄:高中數學O整數系、有理數系，40]頁， I986年8月初版。121林義雄:關於無限大"m"暨其他(將刊登在本雜 誌上)(31林義雄、林紹雄:理論分析初步，九章出版社， I985年5月修訂二版，第一章(特別，p．45 p.93.p.97.)。(4)V．c．Harris:什 歹為無理數的證明，木期。(51G．H．Hardy:PwreMathematics(有翻配本 )，p.68。161林紹雄:極限概念，本期。(71洪萬生:中國n的一頁滄桑，自然科學文化公司， I98]年。(8)華羅庚:數學分析導引，士冊，凡哭出版社，I978 年，p.I04。191林義雄:高中數學O自然數系，I985年8月出版， p.49I。砌馮蘋:高一上數學第一章重點，本期。仰林義雄:幾何學專欄，本期。