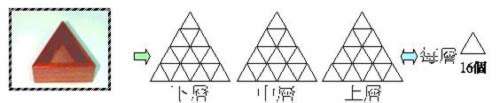
三角柱木盒有三層高，每層面積等於16個單位正三角形。
前言：
"百慕達三角"（Bermuda Triangle）是位於北美洲東南、北大西洋西部，紐西蘭和西印度群島之間的神祕海域，它呈三角形狀，面積廣達４６萬平方公里，三個頂點分別是百慕達、波多黎各及美國的佛羅里達。歷年來在這海域發生了許多不可思議的事，超過50艘船泊、20架飛機突然不明原因地失蹤，並且未留下任何殘骸的痕跡。哥倫布曾提及航行通過此海域之險惡情境。
這件學具是美國Bill Cutler 教授設計的，以"百慕達三角"為名，可見其詭異與艱難。
玩法：
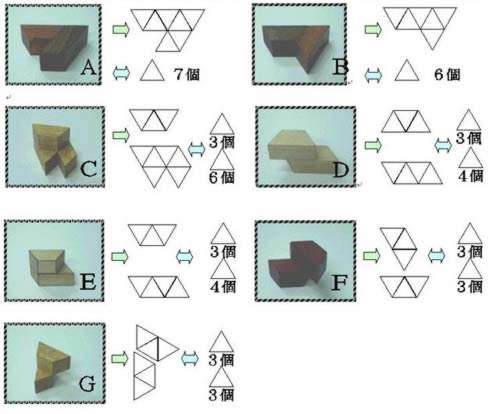
本學具共有7片配件，全部由多個單位正三角形組成，有二片是單層的，其它五片是雙層。我們以一個單位正三角形的面積當作１，則各配件之構造如下：
三角柱木盒有三層高，每層面積等於16個單位正三角形。
因為拼好後，整組翻轉視為結構相同的解答，此時上下層易位，因此，我們不再分辨何者是上層，何者是下層，統稱為外層。
由於這七片配件無法直立放入木盒中，必須是平放，我們可以暫時不考慮高度，只要明確每片配件在三層間的相對位置即可。首先我們從它們面積的關係下手。
A. 用3,4,6,7只有下列5種不同的方法組成16：
| （Ⅰ）3+3+3+3+4 （Ⅱ）3+3+4+6 （Ⅲ）4+6+6 （Ⅳ）3+3+3+7 （Ⅴ）3+6+7 |
因為我們的配件中只有兩片具有4單位正三角形，因此方法(I)、(II)、(III)中只能選兩種；只有1片具有7單位正三角形，因此方法(IV)、(V)只能選一種。 |
A、B這兩片只有一層；C、D、E、F、G各有兩層，其總數有12項，無論如何拼湊，中層都會有5項。因此中間層必須是3+3+3+3+4。3+3+4+6不可以和3+3+3+7搭配在一起(三單位的項數不夠)；4+6+6不可以和3+6+7搭配在一起(六單位的項數不夠)，所以只有下列可能之組合：
| 組合１: | 組合２: |
| (III)：4+6+6+ 7 （外層） | (V)：3+6+7 （外層） |
| (I)：3+3+3+3+4 （中層） | (I)：3+3+3+3+4 （中層） |
| (IV)：3+3+3+7 （外層） | (II)：3+3+4+6 （外層） |
由於A、B之總面積只佔13，無法構成一層，因此，C、D、E、F、G這五片無法全部在同二層中，它必須分別散居三層間。現在我們分別檢驗上述二種情況：
組合１： 4+6+6 3+3+3+7 3+3+3+3+4
我們先從較簡單的4+6+6 這一層開始：拼合B和C這兩片使之能置入木盒的方法有下圖所示的四種方法，其中＜1-1＞、＜1-2＞和＜1-3＞都無法讓E或D填入，只有＜1-4＞留下4個單位的完整的空間，可以繼續填入E或D。
| ＜１－１＞ |  |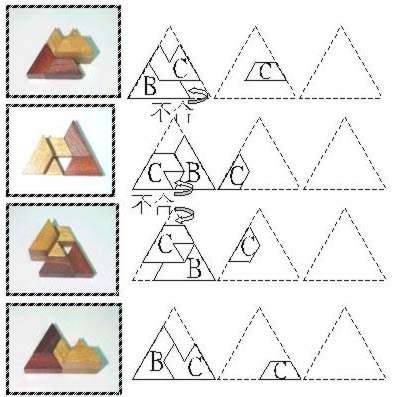
| ＜１－２＞ | |
| ＜１－３＞ | |
| ＜１－４＞ |
剩下4單位的空白，有二種可能的方法填入，加入Ｄ或Ｅ：
| ＜１－４－１＞ |  |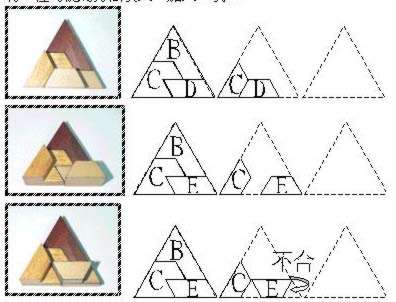
| ＜１－４－２＞ | |
| ＜１－４－３＞ |
無論是情形<1-4-1>或<1-4-2>，在第二層上加入另一片包含有4單位者。
| ＜１－４－１－１＞ |  |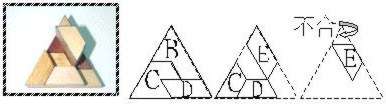
| ＜１－４－１－２＞ |  |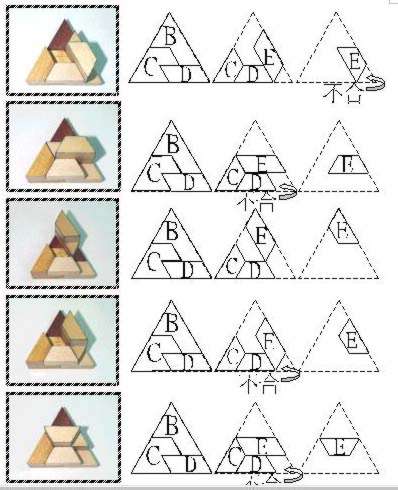
| ＜１－４－１－３＞ | |
| ＜１－４－１－４＞ | |
| ＜１－４－１－５＞ | |
| ＜１－４－１－６＞ | |
| ＜１－４－２－１＞ |  |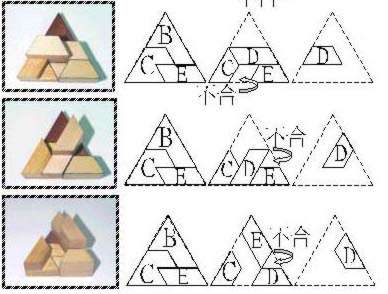
| ＜１－４－２－２＞ | |
| ＜１－４－２－３＞ | |
| ＜１－４－２－４＞ |  |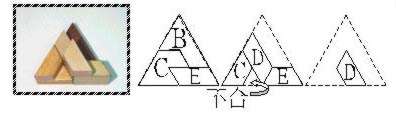
在(1-4-1)的情形，有六個位置可以加入E，即圖(1-4-1-1)、(1-4-1-2)、(1-4-1-3)、(1-4-1-4)、(1-4-1-5)、(1-4-1-6)；其中只有(1-4-1-4)可以再加入F和G (1-4-1-4-1)，最後也沒有辦法放入A了。在(1-4-2)的情形，也有四個位置可加入D，即圖(1-4-2-1)、(1-4-2-2)、(1-4-2-3)、(1-4-2-4)， 但這四種方法都會留下一個單位或二個單位的空間，使後續無論如何放置都無法完成。
＜１－４－１－４－１＞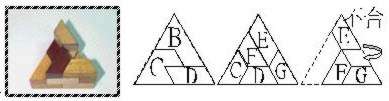 
所以由組合１無法得出任何解答。
組合2： 3 + 6 + 7 3 + 3 + 3 + 3 + 4 3 + 3 + 4 + 6
我們先從3 + 6 + 7這一層開始：
6＋7有二種組合，就是AB或AC。AB又分為三種方式，其中(2-1)與(2-2)都留下二處1單位的空間，使後續無論如何放置都無法完成。AC也分成二種方式，其中(2-4)留下一處1單位空間，另一處2單位的空間，也使後續無論如何放置都無法完成。因此，只有(2-3)及(2-5)可以組成3＋6＋7。
| ＜２－１＞ |  |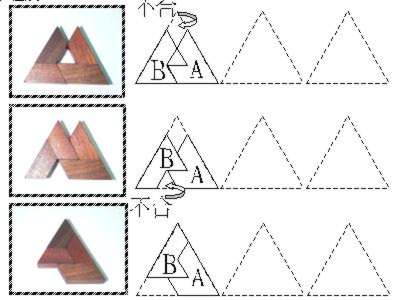
| ＜２－２＞ | |
| ＜２－３＞ | |
| ＜２－４＞ |  |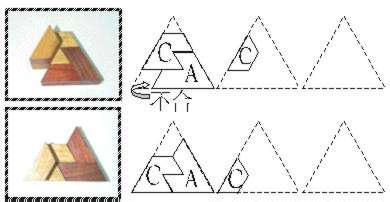
| ＜２－５＞ |
以下先看(2-3)，有下圖5種繼續拼合的情形(2-3-1＆2-3-3＆2-3-5為2-3之翻轉)：
| ＜２－３－１＞ |  |
| ＜２－３－ 2 ＞ | |
| ＜２－３－ 3 ＞ | |
| ＜２－３－ 4 ＞ | |
| ＜２－３－ 5 ＞ |
(2-3-1)與(2-3-5)留下1單位空間，無法完成。(2-3-2)的情形下，無論中層E旁邊如何配置Ｄ、Ｆ、Ｇ，均無法再放入Ｃ繼續拼合完成。
| ＜２－３－２－ 1 ＞ |  |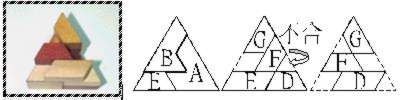
| ＜２－３－２－ 2 ＞ |  |
| ＜２－３－２－ 3 ＞ | |
| ＜２－３－２－ 4 ＞ | |
| ＜２－３－２－ 5 ＞ | |
| ＜２－３－２－ 6 ＞ | |
| ＜２－３－２－ 7 ＞ |  |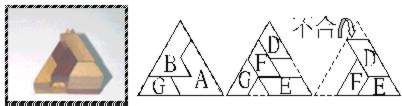
(2-3-3)與(2-3-4)的情形下，C也無法置放於最上層。因此，以上各種拼合方式都無法完成。
再考慮(2-5)的情形：它也只能再加上G和E兩種情形：
| ＜２－５－１＞ |  |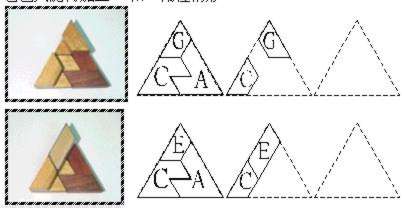
| ＜２－５－２＞ |
在(2-5-1)的情形下，E、F和G最多只能置入二片，再加入B也無法拼合完成。
| ＜２－５－１－１＞ |  |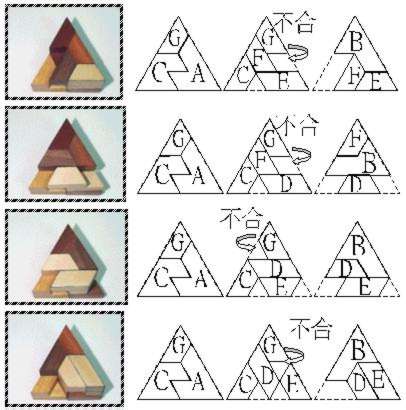
| ＜２－５－１－２＞ | |
| ＜２－５－１－３＞ | |
| ＜２－５－１－４＞ |
(2-5-2)是最後的的一種情形，在中間層留下了9單位的正三角形空間，剩餘的D、F、G有以下三種拼合成正三角形的方法：(3-1)、(3-2)無法使B再加入拼合，(3-3)是唯一的一種可以使B拼入的組合情形，拼入B後就成為(3-3-1)。
| ＜３－１＞ |  |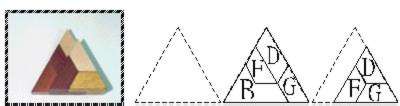
| ＜３－２＞ | |
| ＜３－３＞ | |
| ＜３－３－１＞ |
接著將(3-3-1)翻轉，再與(2-5-2)拼合，所得到的結果就是置入正三角形木盒的唯一解。
＜"百慕達三角"解答＞
如果沒有運用數學方法分析而盲目地嘗試，將會浪費很多時間。運氣好碰巧完成了，再把它弄亂了，又無法再很快地完成了！
我們把解題過程簡要地用以下的樹狀圖表示之：
第一種組合：(4+6+6)＆(3+3+3+7)＆(3+3+3+3+4)
由(4+6+6)這層開始
第二種組合：(3+6+7)＆(3+3+3+3+4)＆(3+3+4+6) 由(3+6+7)這層開始
