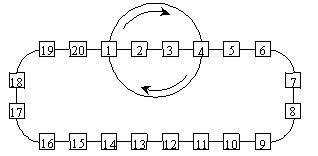

可以先考慮怎樣將5移到最前面(其它數的順序不變),即將1,2,…,20變為5,1,2,3,4,6,7,…,20?
用箭頭表示一次顛倒順序,稱為一步,通過嘗試,不難得出:
12345→15432→34512→32154→51234
總結一下:每一個數(例如5),可以通過4次顛倒,向前移4位。這4步,我們簡記4→。
採用這種方法,將6向前移四位,再移四位,…,這樣移六次(共24步),在方塊數為20時,如圖二,最後的次序變成6,1,2,…,20。
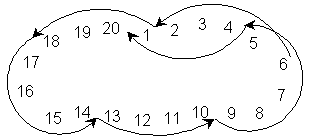
同樣地,對18個方塊,採用上面的方法將6前移四位,移14次(共56步)後,方塊的次序就變成6,1,2,…,18。
對排成
1,2,…,19 (1)
的19個方塊,情況與上面迥然不同,無論多少步,也不能使它的順序變成
6,1,2,…,19 (2)
為了說明這一點,我們注意:在(2)中,6越過了五個數:1,2,3,4,5。即6與這五個數的次序顛倒了,稱為5個逆序。而在(1)中,沒有逆序,即逆序個數是0。
由於在圓周上,最後一個數也可以作為第一個數,例如(2)也就是
19,6,1,2,…,18 (3)
19寫在前面,產生18個逆序,所以(3)有23個逆序。但(2)、(3)的逆序數都是奇數,即使將18,或者17、16等也寫在前面,標出來的逆序數仍然是奇數。而(1)的逆序數總是偶數,不論19(或18、19或17、18、19等)是否寫在前面。
每顛倒四個數的順序一次,逆序數的奇偶性不變,因為4,3,2,1 中逆序數是3+2+1=6,是一個偶數。所以,無論經過多少步,(1)中逆序數始終是偶數,而(2)的逆序數是奇數,(1)不會變成(2)。