
I. 索瑪誕生的故事
1969夏,派克兄弟公司(Parker Brothers Inc.)首度將索瑪立方塊上市。在此之前,馬丁•嘉德納(Martin Gardner)曾撰文在《科學美國人(Scientific
American)》的數學遊戲專欄中介紹過,並使它風靡全球。索瑪立方塊可以用來協助人們增進空間關係的思維技能,它能讓人們沈迷數小時享受探索的樂趣。
索瑪立方塊是由丹麥亞特•海恩(Piet Hein)發明的。1936年,皮亞特•海恩在聆聽偉納•海森伯格演講“量子物理”的場合,構思出索瑪立方塊的。當時這位德國物理學家正在講述把空間切割成立方體。皮亞特•海恩敏銳的想像捕捉到以下的幾何原理:
將四個以內,大小相同的立方體,以面相連接,構成的所有不規則形狀,可以重組成一個較大的立方體。
海森伯格還在演講,海恩已經很快地在紙上塗塗畫畫,確定這總體積為27個單位的七片形狀可以組成一個3x3x3的立方體。演講結束後,他把27個立方體黏成這七個形狀,並很快地證實他的想法。索瑪立方塊從此誕生。
II. 皮亞特•海恩小史

皮亞特•海恩(Piet Hein, 1905-1996)是具有廣泛興趣的丹麥詩人及科學家。他的詩集在丹麥以筆名“Kumbel”著稱,擁有數百萬計的讀者。他最有名的詩集叫“Grooks”,這是他在1940年當納粹侵佔丹麥時寫的。當時他是反納粹組織的首領,組織轉入地下活動後,他致力寫詩。根據資料,Grooks賣了7000多本,當時麻省理工學院出版社在美國出版此詩集後,它一度榮登紐約時報暢銷書排行榜。
皮亞特•海恩具有多方面的天才。除了發明索瑪立方塊外,他也創建了一個新的幾何型體──“超橢圓”,它近似於長方形及橢圓之間,這個型體也可以成為三度空間稱之為「超級蛋」或「超級橢圓體」。
在五十到六十年代,皮亞特•海恩從事藝術及建築工作,他設計了一些造型優美的傢俱並努力推展「北歐設計」的商品形象,使他成為國際精品的表徵。在國際上,他經常試圖在「硬」的科技與「柔」的人文之間建立橋樑。
皮亞特•海恩的創造力證明他是思維聰穎縝密的人──用他的左腦創造索瑪立方塊及超橢圓,用他的右腦創作詩集及散文。他在數學及科學上的貢獻可與波爾(Niel
Bohr)與愛因斯坦(Albert Einstein)並駕其驅。事實上,他曾與愛因斯坦共事多年,也曾是哥本哈根的波爾研究所的一員。
不僅是皮亞特•海恩如此傑出聰明,他的父親是個土木工程師,其最著名的設計是哥本哈根Tivolo遊樂園的雲霄飛車。他的母親是位眼科醫師。皮亞特•海恩有二個兒子都熱愛索瑪立方塊,並有專業的研究,作出許多漂亮的造型及證明。
III. 認識索瑪的配件
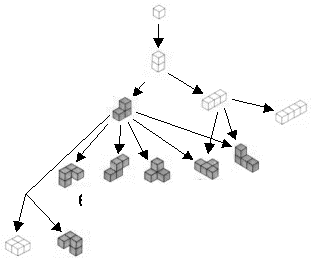
索瑪的基本結構是單位正方體。如上圖,二個單位正方形以面相連接,只有一種形狀(旋轉、翻轉視為相同),但它是規則長方形,不符合皮亞特•海恩的設計原意,故不採用。三個單位正方形以面相連接,有二種形狀,但左邊成I
字型的那片是長方體,不採用。四個單位正方形以面相連接,有八種形狀,其中I 字型及田字型是規則形狀,亦不採用。下圖有陰影的七片,就是索瑪的組件。
我們鼓勵大家自己動手依上圖樣式製作索瑪,只需要將木頭切成小立方塊,然後在表面上塗上黏膠(建議用白膠)再黏合即可。
這七片組件的總體積為27單位,可以重拼成3x3x3的正立方體。
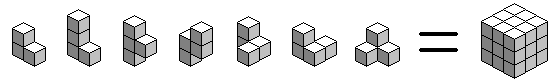
註:所謂“不規則型狀”在數學上稱作凹多面體──多面體上能找到相異的二點,使得此二點的連線除了兩端點外不在多面體內部。長方體任二點的連線都在它的內部。
IV.索瑪的編號與配色
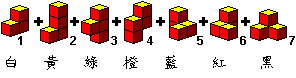
為了方便對索瑪進行研究及記錄,我們把每片組件編上號碼,此編號是國際通用的,您只須用編號而不用繪圖就可和全世界的索瑪迷進行交流。彩色索瑪的配色方法是採用Conway的建議,它便我們對拼出的作品進行分類。
另外,我們把七片索瑪用黑、白相間塗色,這可以方便我們作一些數學證明。
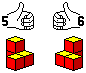 如果你困惑於辨認那片是5號?那片是6號?我們教你一個簡易的辨認規則:豎起大姆指,則5號的形狀像我們的左手,6號的形狀則像右手,阿拉伯數字的寫法依序是由左到右的,所以左=5,右=6。
3號及4號的外型很像阿拉伯數字的3和4,應不難辨認。1號、2號都是L形,1號是最小的3單位那片;2號則是4單位那片。剩下的7號無論從那個方向翻轉,它都是對稱的。
如果你困惑於辨認那片是5號?那片是6號?我們教你一個簡易的辨認規則:豎起大姆指,則5號的形狀像我們的左手,6號的形狀則像右手,阿拉伯數字的寫法依序是由左到右的,所以左=5,右=6。
3號及4號的外型很像阿拉伯數字的3和4,應不難辨認。1號、2號都是L形,1號是最小的3單位那片;2號則是4單位那片。剩下的7號無論從那個方向翻轉,它都是對稱的。
V.索瑪解答的記號
為了便於記錄拼完成的圖形,國際上通常以此圖形的正投影作為圖形的基底,由最上層至最底層,逐一在相對位置上填入索瑪組件的編號,空白的部份用黑點代表(不會導致混淆時亦可省略)。有空洞的位置寫上0或•。如果圖形是由二套索瑪拼成,則第二套索瑪用V,L,T,Z,A,B,P作為編號。這些記號稍加變化即可變成電腦也能讀懂的語言。例如下圖之記錄方法為:
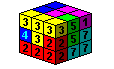
| 上層 | 中層 | 下層 | |
| 4 1 1 | 6 5 7 | 6 7 7 | 後面 |
| 4 1 5 | 4 5 5 | 6 6 7 | |
| 3 3 3 | 4 3 2 | 2 2 2 | 前面 |
下圖的記錄方法為

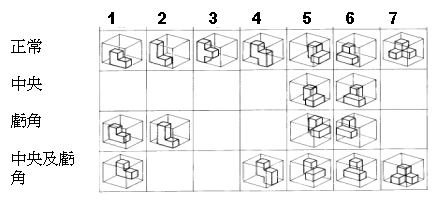
VI.索瑪拼圖
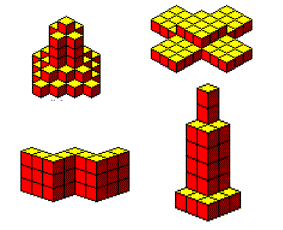
 簡單的七片索瑪組件,可以構造變化萬千的圖形,有動物、傢俱、建築、飛機……等可愛的造型。
簡單的七片索瑪組件,可以構造變化萬千的圖形,有動物、傢俱、建築、飛機……等可愛的造型。
索瑪拼圖的基本技巧是試著以其中兩片拼成下圖之階梯式樣。
下右圖可用索瑪組件中的3片拼成, 而下左圖則另外的4片拼成。

如果取出最小的1號這片,用其它的6片可以拼成與它相似,且放大為2倍的造型。
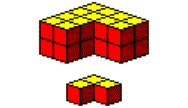
掌握上述的小問題後,便可試著用七片組成3x3x3立方體,這是索瑪最簡單的造型之一。它有非常多種拼法,建議您至少要熟練一種拼法,否則您將不易在短時間內收拾好它。
下面是一個非常特別的構造方法,先用其中的3片及4片拼成下一圖形,再將2個圖形合併在一起即可。
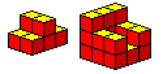
下面我們列出許多迷人的造型,請您試著拼出它們,並記錄下您的答案;您會發覺其中趣味無窮。請慢慢享受吧!
VII.兩組索瑪的拼圖
 利用兩組索瑪一起拼圖,不僅挑戰難度加大,樂趣也加倍。
利用兩組索瑪一起拼圖,不僅挑戰難度加大,樂趣也加倍。
例如右圖之解答為:
VIII.索瑪的數學
A.可以放在什麼位置?
當我們用索瑪拼圖時,最常用的方法是嘗試錯誤,先用一片定位(最上策是挑選較不規則且必須佔兩層的5號、6號、7號),然後試著逐一將其它幾塊嵌入,錯了從頭再來過。用嘗試錯誤的方法如果運氣好正好碰上了,很快就可拼成,有時運氣不佳,試了很久仍不得其門,甚至經常重複之前試過的步驟,一再犯錯而不自知。如果能仔細觀察與作些數學分析,將使您嘗試的步驟減少很多,並避開一些明顯的錯誤,使事半功倍。
我們以拼成3x3x3的正方體為例。一個正立方體有6個面、8個頂點、12條邊。我們若把頂點所在的8個單位立方體塗上黑色,則索瑪的各組件能佔住角落的數量如下表:
| 組件編號 | 1號 | 2號 | 3號 | 4號 | 5號 | 6號 | 7號 |
| 可能佔住角落數 | 0或1 | 0或1 2 | 0或2 | 0或1 | 0或1 | 0或1 | 0或1 |
如果3號組件佔住0個角落,則即使2號佔住2個角落,其它的組件各佔住1個角落,則全部組件最多也只能佔住7個角落,這樣就無法拼出有8個角落的正立方體。因此,3號組件必須佔住2個角落,也就是說,它必須放置在邊緣的位置上(如下圖)。
我們若把3x3x3的立方體,黑白相間塗色,並使角落塗上黑色,則此立方體有14個單位立方體是黑的,13個是白的。把索瑪的7片組件置入,其所佔位置的黑白數量可能值如下表所示:
| 組件 | 1號 | 2號 | 3號 | 4號 | 5號 | 6號 | 7號 | 總數 |
| 黑 | 2或1 | 2 | 3或1 | 2 | 2 | 2 | 3或1 | 14 |
| 白 | 1或2 | 2 | 1或3 | 2 | 2 | 2 | 1或3 | 13 |
由表中可知組件2號、4號、5號、6號無論放置在那個位置,都會佔住2黑2白。由前面的結論得知,3號組件必須放置在邊緣上,也就是說,它必須在佔有3黑1白的位置。目前,2號、3號、4號、5號、6號等5片組件共佔住11黑9白。由此推論,1號及7號組件必須佔3黑4白,可得知,7號必須佔住1黑3白,1號必須2黑1白,否則將不合。
這個結論也告訴我們1號至7號組件可能擺置的位置只能如下圖:
經過了以上的分析,我們了解每片索瑪可能放置的位置,這將對您有莫大助益,避免許多明顯的錯誤,節約許多時間。您也可以作進一步的分析,縮減須嘗試的組合數,歡迎將您發現的結果寄給我們分享。
B.有多少組解?
尋求某個索瑪拼圖共有多少組結構完全不同的解,是非常有趣的數學問題。要證明這類的問題並不容易,首先你要實證所宣稱的每一個解都可以達成,然後,你必須證明沒有其它的解。
在派克兄弟公司的索瑪手冊上宣稱:John Horton Conway和M..J.T. Guy二位劍橋大學的數學家,首先提出將索瑪組成3x3x3立方體的方法冇240種結構完全不同的解,並經過電腦程式證實。事實上,Conway和Guy兩人是在一個下雨的午後,閒著沒事,用雙手拼解出來的。Conway特別強調:“我認為像索瑪這種尺寸,若要用到電腦,就等於承認挫敗了。只要找到正確的方法,用雙手完成比設計程式要快多了。”
Conway和Guy兩人後來發現,由239種解法(有一個解法異常)中的任一種開始著手,其餘的238種解答,可經由每次改動三片以下的組件而逐步解出。Conway並畫了一大張圖表(他稱之為索瑪譜),顯示這239種解法彼此之間的關聯。在他倆合著的《Winning
Way》書中第802、803頁可找到此圖譜。
一個正立方體的對稱立方體有48個(假設固定最上層的面,經旋轉有4種,6個面均可翻轉到最上層,如此即有24種。每一種都有一個鏡面倒影(Mirrow
image),故共有48種)。相同的位置上,7號組件有三種對稱的放置方式,1號、3號、4號、5號、6號組件各有2種對稱的放置的方式。因此,拼成3x3x3立方體如果不論結構是否相同,其所有解答的個數為240x48x3x2x2x2x2x2=1105920。
對於將索瑪組成3x3x3立方體的方法冇240種結構完全不同的解這個結論,新竹市光華國中一年級的賴俊儒小朋友有不同的見解。他在一篇文章中寫道:「去年暑假在九章數學俱樂部(遊戲中的數學)活動中,我第一次接觸到索瑪立方這個玩具,玩了之後我很驚訝,簡簡單單的七種組件卻可以變化出多樣的造型,我用了一個禮拜的時間拼完卡片上所有的造型,還設計了幾個新造型投到索瑪立方的網站。那時候全家愛玩的遊戲是隨便抽一張卡片,然後用計時器計時,比賽誰排得最快,最常見的結果是我第一,媽媽殿後。
有一回,聽孫文先先生提到有關文獻說索瑪立方體有240種不同結構的組合方法,當時,我就想試試看能不能將這240種排法排出來。在徵得爸媽的支持後,我們先向木工廠訂了三種不同單位的木塊由媽媽和姊姊製成七種不同的組件,爸爸再漆成不同顏色,全家開始向索瑪立方體挑戰。
按照計劃我一種一種的去嘗試組合,起初進度較慢,不大順手,等我熟悉七種組件間的關聯和變化後,組合成功的立方體就迅速增加,可是隨著組合的增多,重複出現的情況也多了,在拼拼拆拆下目前我已排出四百七十幾種組合。現在我和家人最常作的一件事就是望著擺著地板上的立方體發呆,企圖找出重複的組合或排出新組合。
有一次我作夢,夢見滿地的索瑪立方體在翻滾─恐怖!! 」
後來,他拼湊出476種不同的解。最近,他以索瑪為題作了一件科展作品,把480種解法全部找出,並加以系統分類及繪製了兩大張“索瑪圖譜”。他認為索瑪組成3x3x3立方體結構完全不同的解法應為480種,把鏡面倒影視為相同是不合理的。
他的理由為:
(1)某組解的鏡面倒影必須把5號組件及6號組件互換。如此,兩組解各層的記錄數字記號不同。
(2)海恩對索瑪的定義是:There are seven soma pieces composed of all the irregular face-joined cubes (polycubes) with ≦ 4 cubes. The object is to assemble the pieces into a cube. No two shapes are alike, although 5 and 6 are mirror images of each other.他明確指出組件5與6是不同的兩種組件,若將鏡像當作相同則與定義不符。
(3)索瑪立方體是實物而非影像,以物理學而言,實物與虛像很難視為相同。
(4)我們不能照著鏡子,切下左右手互換,再認為鏡中是同一人。
在數學上,我們經常把同性質的物件算為一類。Conway當然可以把鏡像的解計數為同一類。因此,我們宣稱索瑪拼成3x3x3正立方體的解時,應加上註解:
如果把它的鏡像視為相同,則有240種結構不同的解。或:如果把它的鏡像視為不相同,則有480種結構不同的解。
如果把索瑪的組件依下圖方式黑白相間塗色,請問黑白相間且頂點為黑色的3x3x3正立方體結構不同的解有多少種?如何證明?

美國Design Science Toys公司出品了一組斜索瑪,它把索瑪立方塊設計成傾斜的,它的每個面都變成菱形的,數學上稱它為菱形體。該公司宣稱它結構不同的解答只有一種,你相信嗎?你能證明嗎?

C.可不可能拼成?
並不是任何體積為27單位的圖形都可以用索瑪拼成。例如下圖即不可能拼出。

它不可能用索瑪拼出的證明是由加州理工學院噴射推進實驗室的數學家所羅門•W.哥隆(Solomon W. Golomb)首先發現的。他將圖形的底盤,依下左圖的方式黑白交錯塗色,底盤塗黑色之上的整柱小立方塊都塗黑色,底盤塗白色之上的整柱小立方塊都塗白色。全圖形共有19個黑色,8個白色。
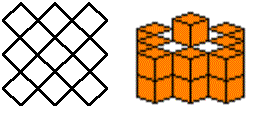
他的證明是:檢視七片索瑪,以各種方向把它們一一放在圖形內,求取它所佔黑色方塊最大數目,此時,它佔用白色方塊數最少。以下統計表列出了每一塊的可能數:
| 索瑪編號 | 最多佔用黑色方塊數 | 最少佔用白色方塊數 |
| 1 | 2 | 1 |
| 2 | 3 | 1 |
| 3 | 3 | 1 |
| 4 | 2 | 2 |
| 5 | 3 | 1 |
| 6 | 3 | 1 |
| 7 | 2 | 2 |
| 總 計 | 18 | 9 |
D.放多少片?
X.與索瑪有關的網站
http://www.netpower.no/~ranveig/piethein/soma.html
http://www.fam-bundgaard.dk/SOMA/SOMA1/SOMAFIG1.HTM
http://w.w.w.ctaz.com/~dmn1/soma.htm
http://www.highland.madison.k12.il.us/jbasden/somacube/constructbw.html